線形近似曲線の概要
「線形近似曲線」、または「最小二乗法による直線フィッティング」は、データのパターンを一本の直線で表現しようとする手法です。散布図上の各点からその直線までの垂直距離(残差)の二乗和が最小になるような直線を求めます。これにより、観測データの背後に存在すると考えられる直線的なトレンドやパターンを見つけ出すことができます。
エクセルでは、線形近似曲線(または「トレンドライン」)をグラフに追加することで、データセットの全体的な傾向を視覚化することができます。これは、単にデータポイントをプロットするだけでは見えにくい傾向やパターンを明らかにするのに有用です。
以下は、線形近似曲線を用いる具体的なシーンです:
- 予測と予測: 線形近似曲線は、未来の値を予測するために使用されます。例えば、過去数年間の会社の売上データがあるとします。これらのデータに基づいて線形近似曲線を作成すれば、次の年の売上を予測するのに役立ちます。
- 相関の確認: 二つの変数間の関係性を評価するために線形近似曲線を使用することがあります。これは、ある変数の変化が他の変数にどのように影響を与えるかを理解するのに役立ちます。例えば、広告費と商品の売上の関係を調べる場合、線形近似曲線を使用すると、広告費が増加すると売上も増加するかどうかを視覚的に確認することができます。
エクセルで線形近似曲線を描く方法は、散布図を作成した後、グラフ上で右クリックし、「トレンドラインの追加」を選択することで実現できます。その後、トレンドラインの種類として「線形」を選択すれば、データに最適な直線が描かれます。
具体的な使用シーン
エクセルの散布図に線形近似曲線を追加すると、以下のようなシーンで分析に役立ちます:
- 売上予測: ある会社が過去数年間の売上データを持っているとします。売上をY軸に、時間(年)をX軸に取って散布図を作り、そこに線形近似曲線を追加すれば、将来の売上予測が可能になります。予測精度はデータの一貫性や線形近似曲線のフィット具合によるため、必ずしも100%正確ではありませんが、大まかな予測として有用です。
- 広告効果の分析: 例えば、広告費用と売上との関連性を見たいときには、広告費をX軸に、売上をY軸に取って散布図を作り、線形近似曲線を追加します。これにより、広告費が増えると売上が増えるか、それとも広告費が増えても売上に大きな影響を与えないかなどの傾向を視覚的に理解することができます。
- 製品の品質管理: 製品の製造過程で、あるパラメータ(例えば、温度)が製品の品質(例えば、不良率)にどのように影響するかを確認したい場合、そのパラメータをX軸に、品質指標をY軸に取って散布図を作り、線形近似曲線を追加します。これにより、パラメータの微調整が品質改善にどの程度貢献するかを評価できます。
- 経済指標の分析: GDP(国内総生産)と失業率の関係など、マクロ経済の指標間の関係を理解するために線形近似曲線を使用することもあります。これらの指標を散布図にプロットし、線形近似曲線を追加することで、一方の指標が増加すると他方の指標がどのように動くかを視覚的に把握することができます。
エクセルで試してみよう
「近似曲線の追加」や「線形近似」の設定に適したサンプルデータを作成します。以下のように考えてみましょう:
| 年(年) | 売上(百万円) |
|---|---|
| 2014 | 200 |
| 2015 | 240 |
| 2016 | 220 |
| 2017 | 260 |
| 2018 | 240 |
| 2019 | 290 |
| 2020 | 260 |
| 2021 | 310 |
| 2022 | 280 |
| 2023 | 300 |
このデータは、年ごとの売上が線形に増加しているというシンプルなデータです。
次に、このデータを使ってエクセルで散布図を作り、線形近似曲線を追加する手順を説明します:
- まず、エクセルを開き、上記のデータをシートに入力します。
- 入力したデータを全て選択します。
- [挿入]タブをクリックし、[散布図]のボタンをクリックします。出てきたメニューから、マーカーのある散布図(最初のオプション)を選択します。これで基本的な散布図が作成されます。
- この散布図に線形近似曲線を追加するには、散布図のどこかをクリックして選択し、表示されるデザインメニューから[グラフ要素の追加](+ボタン)を選択します。
- [グラフ要素の追加]メニューから、[近似曲線]を選択します。このとき、さまざまな種類の近似曲線の中から「線形」の近似曲線を選択します。これで散布図に線形近似曲線が追加されます。
- また、近似曲線の数式やR²(決定係数)を表示するには、近似曲線を右クリックし、「近似曲線の書式設定(オプション)」を選択します。表示されるダイアログボックスで、「グラフに数式を表示する」と「グラフにR-2乗値を表示する」のチェックボックスをオンにします。これで数式とR² 値が散布図上に表示されます。
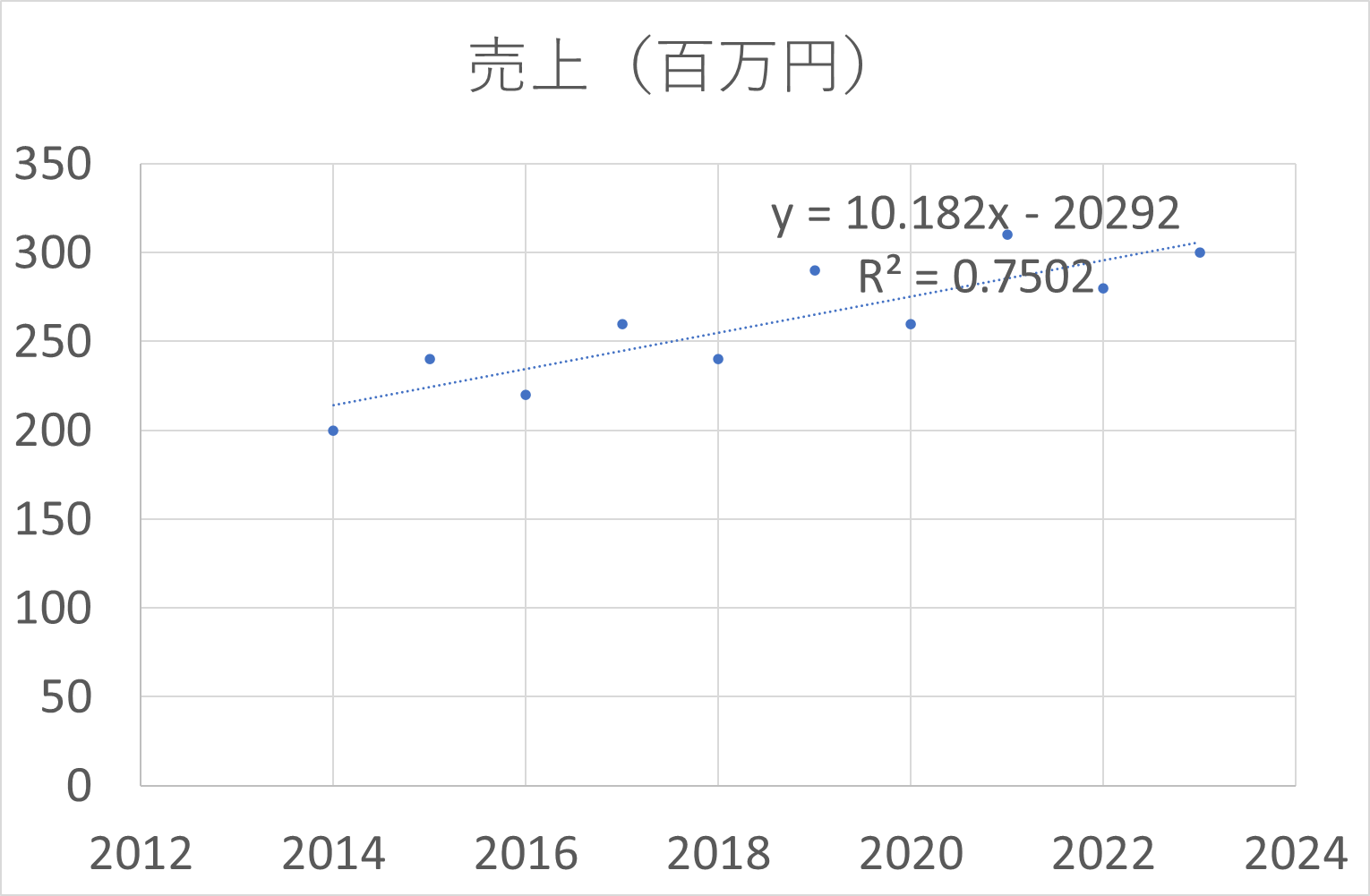
線形近似曲線の数式:「y = ax + b」形式の一次関数
エクセルで表示される近似曲線の数式「y=10.182x – 20292」について説明します。
まず、数式の一部「y=10.182x – 20292」は、所謂「y = ax + b」形式の一次関数を表しています。この一次関数は直線の方程式で、その直線はデータポイント(散布図上の各点)の傾向を示す「最適な」直線を描いています。エクセルが計算するこの直線は「最小二乗法」を用いてデータとの間に残差(観測値と予測値との差)の二乗和が最小になるように決定されます。
この数式における各部分の意味は次の通りです:
- ‘y’は予測された売上を示します。
- ‘x’は年を示します。これは独立変数(原因または入力)です。
- ‘10.182’は近似直線の勾配を示します。これは一年につき売上が平均で約10.182百万円増加することを示します。つまり、これが売上の年間増加率を表しています。
- ‘-20292’はy軸と近似直線が交差する点、つまりy切片を示します。物理的な意味を持たないことが多いですが、ここではx(年)が0のときの売上の値を示します。しかし、我々のケースでは、0年は存在しないため、この値は解釈が難しいです。
この数式が示すものは、年数が1年増えるごとに売上が平均で約10.182百万円増加するという売上の一般的な傾向です。しかしながら、現実のデータはノイズを含んでおり、全ての点が完全に一直線上にはならないため、各データ点と近似直線との間には差があります。この差が小さいほど、近似直線がデータの傾向をよく表現していると言えます。
「y=10.182x – 20292」は、その傾向を数式化したもので、新しい年(xの値)をこの数式に入力することで、その年の売上予測値(yの値)を計算することができます。ただし、この予測は過去の傾向に基づいているため、未来が過去と同じ傾向を持つとは限らないことに注意が必要です。
