Excel関数を使った離散分布に基づく乱数の生成
1. はじめに
離散分布とは、個別の値を取る確率変数の分布を指します。例えば、サイコロを振ったときの目や、コインの表裏などがこれに当たります。この記事では、Microsoft Excelを使用して、離散分布に基づく乱数を生成する方法を解説します。Excelの関数を使うことで、特定の離散分布を持つデータのシミュレーションを簡単に行うことができます。
2. 離散分布の基本
離散分布は、個別の値が取られる確率を具体的に示したものです。たとえば、公正なサイコロを投げた場合、1から6までの各目が出る確率は1/6です。これは離散的な値（サイコロの目）とその出現確率を示した典型的な離散分布です。他にも一定の割合の当たりがでるくじ引きなどです。
離散分布は、ビジネスの予測、科学研究、ゲームの結果のシミュレーションなど、さまざまな現実のシチュエーションで使われます。たとえば、製品の販売予測をする際、特定の個数が売れる確率を離散分布として表現し、その分布に基づく乱数を生成することで、さまざまな販売シナリオをシミュレートすることが可能です。
3. 離散分布に基づく乱数の生成
Excelでは、RAND関数とMATCH関数、INDEX関数を使って、離散分布に基づく乱数を生成することができます。ここでは、ある離散分布に基づいて乱数を生成するための具体的な手順を説明します。
下記のサンプルはくじ引きの出現頻度です。特等～3等が「1:10:50:200」の割合で出現します。そして出現頻度のB列をキーとして昇順に並べています。
| 値 | 出現頻度(比) | 確率 | 累積確率 |
|---|---|---|---|
| 特等 | 1 | ||
| 1等 | 10 | ||
| 2等 | 50 | ||
| 3等 | 200 |
- まず、各値が出現する確率を計算します。これは、その値の出現頻度を全体の出現頻度で割ることで求めることができます。
C列にはC2に「B2/SUM(B:B)」の式を作成し下へコピーします。
- 次に、累積確率を計算します。これは、最小の値から順にその値までの確率を足し合わせたものです。最初の値の累積確率は0とします。
D列ではまずD2に「0」を入力しました。D3には「SUM($C$2:C2)」の式を作成しコピーします。 - 最後に、以下のようなExcelの関数を使って乱数を生成します。
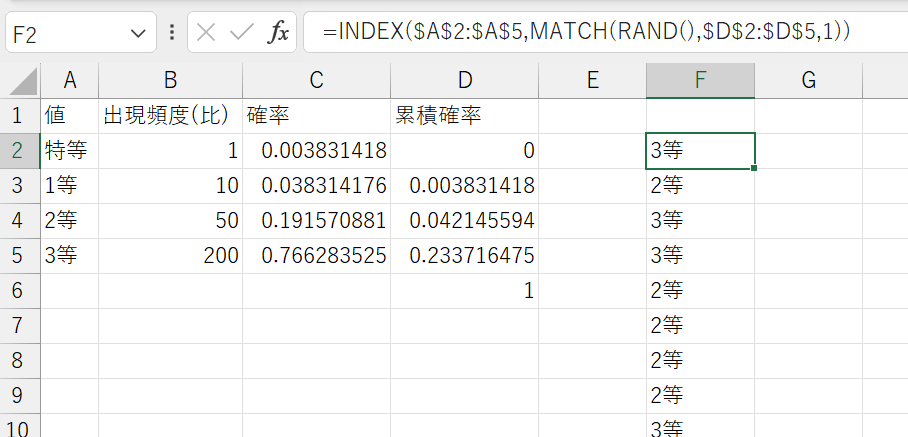
=INDEX(A2:A5,MATCH(RAND(),D2:D5,1))
ここで、A2:A5は値が格納されている範囲、D2:D5は累積確率が格納されている範囲です。この関数を評価すると、指定した離散分布に基づいて乱数が生成されます。RAND関数が0～1の乱数を生成していることを利用した式です。
=INDEX(A2:A5,MATCH(RAND(),D2:D5,1))| 値 | 出現頻度(比) | 確率 | 累積確率 |
|---|---|---|---|
| 特等 | 1 | 0.0038 | 0 |
| 1等 | 10 | 0.0383 | 0.0038 |
| 2等 | 50 | 0.1916 | 0.0421 |
| 3等 | 200 | 0.7663 | 0.2337 |
4. まとめ
この記事では、Excelを使った離散分布に基づく乱数の生成方法について解説しました。離散分布は、個別の値が特定の確率で出現する現象を表現するのに便利なツールです。そして、Excelの関数を使うことで、これらの離散分布を基にした乱数を簡単に生成し、現実のシチュエーションをシミュレートすることが可能です。
参考：離散分布に基づく乱数を生成するユーザー定義関数
頻繁にこの操作をする方は、ユーザー定義関数の登録も検討してください。
コメント