ゴールシークとソルバー
「ゴールシーク」と「ソルバー」は両方ともExcelの最適化ツールですが、それぞれが適する問題の種類や利用シーンが異なります。以下にそれぞれの特徴を詳しく説明します。
ゴールシーク(Goal Seek) ゴールシークは、「ある特定の結果を達成するために、どのように入力値を調整すればよいか」を求めるためのシンプルな最適化ツールです。このツールを使用すると、1つの変数を調整して、特定のセルの結果が目標の値になるようにすることができます。
例えば、販売数と価格から利益を計算するシミュレーションを行っているとします。利益が一定の目標値に達するためには、価格をどの程度に設定すればよいかをゴールシークで求めることができます。
ゴールシークは「データ」タブの「What-IF 分析」から起動できます。
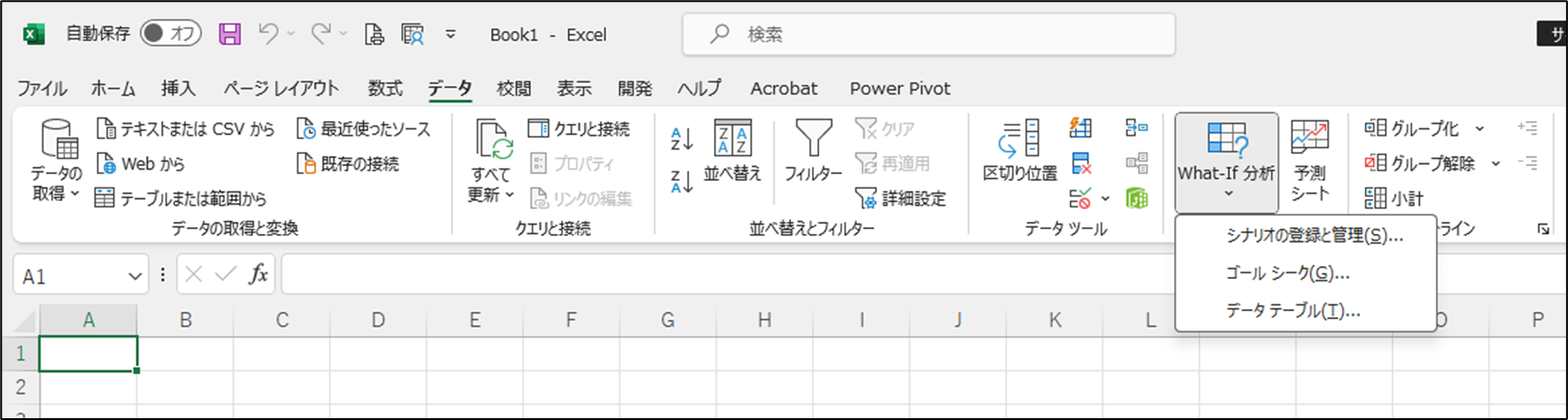
ソルバー(Solver) 一方、ソルバーはより複雑で強力な最適化ツールです。複数の変数や制約条件を持つ問題に対して最適な解を見つけることができます。また、最大化、最小化、特定の値への調整など、目標の種類も選べます。
例えば、製品の製造に必要な原材料のコスト、使用可能な原材料の量、製品の販売価格など複数の変数と制約がある場合、利益を最大化するための最適な原材料の使用量や製品の販売価格をソルバーで求めることができます。
したがって、問題が単一の変数と単純な目標に関するものであればゴールシークを、複数の変数と複雑な目標や制約が関わる問題であればソルバーを使用すると良いでしょう。
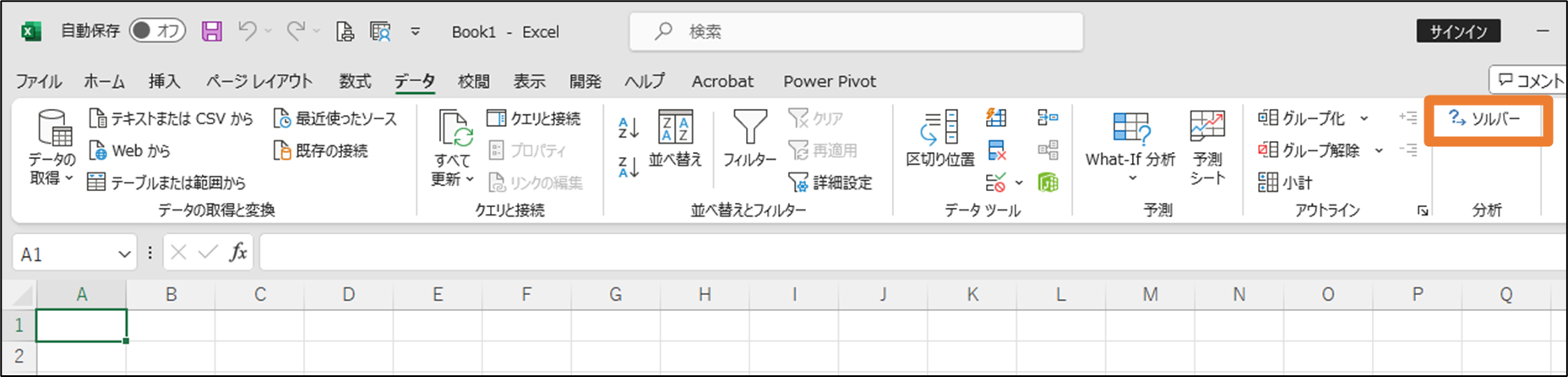
ただし、ソルバーはExcelのアドインとして提供されていて、使用する前に設定で追加する必要があります。「ファイルタブ」の「オプション」から「アドイン・設定」で「ソルバーアドイン」を追加した後、「データ」タブから利用可能になります。
ゴールシークの具体例
具体例1
以下にゴールシークを使用するシナリオの一例を示します。この例では、製品の販売に関するシナリオを考えます。
表1. 製品の販売データ
| 項目 | 値 |
|---|---|
| 製品の価格($) | 100 |
| 販売数量(個) | 500 |
| 総売上($) | 50000 |
この場合、「総売上を60000ドルにしたいが、販売数量は変えずに製品の価格をどのように変更すれば良いのか?」という問題が生じます。このような問題はゴールシークを使用して解くことができます。
ただし事前に「総売上」のセルに「製品の価格*販売数量」の計算式を設定しておく必要があります。(例:B4セルへ「=B2*B3」を設定)
実行時には、Excelの「データ」タブの「予測」グループにある「What-IF分析 ゴールシーク」を選択します。その後、「数式入力セル」に「総売上」セルを、「目標値」に60000、そして「変更させるセル」に「製品の価格」セルを指定します。これにより、目指す総売上に到達するために必要な製品の価格を計算できます。
具体例2
別の一例を示します。この例では、貸付金に対する返済計画について考えます。
表2. ローン返済データ
| 項目 | 値 |
|---|---|
| ローンの元金($) | 20000 |
| 年間利率(%) | 5 |
| 返済期間(年) | 5 |
| 年間返済金額($) | 4500 |
この場合、「年間返済金額を4000ドルに抑えたい場合、返済期間を何年にすれば良いのか?」という問題が生じます。このような問題はゴールシークを使用して解くことができます。
ただし事前に「年間返済金額」のセルに算出用の計算式を設定しておく必要があります。このローン返済データの表において、「年間返済金額」は元金、年間利率、返済期間に基づいて計算されます。具体的には、年間返済金額は等额年金法に基づいて計算でき、ExcelのPMT関数を使うと容易に計算できます。
=PMT(年間利率, 返済期間, ローンの元金)
このローン返済データの例に合わせて、セルを指定すると以下のようになります:
=PMT(B3/100, B4, B2)
これをセルB5(年間返済金額)に入力します。ただし、PMT関数は通常、結果を負の値で出力するため(支払いを表すため)、結果を正の値にするためにはこの式全体をマイナス符号で囲むか、PMT関数の結果にマイナス符号をつけます。したがって、最終的な式は以下のようになります:
=-PMT(B3/100, B4, B2)
実行時には「数式入力セル」に「年間返済金額」セルを、「目標値」に4000、そして「変更させるセル」に「返済期間」セルを指定します。これにより、希望する年間返済金額に到達するために必要な返済期間を計算できます。
ソルバーの具体例
具体例
ソルバーを用いるべき具体例として、製品の最適な生産量を決定する問題を考えてみましょう。各製品には、一定の製造費用と利益があり、それらが互いに異なる制約(例えば、使用可能な原材料の量や工場で使える機械の時間など)を満たさなければならないとします。
表3. 製品の生産データ
| 製品 | 利益 | 原材料の必要量(kg) | 生産時間(h) | 生産量 |
|---|---|---|---|---|
| 製品A | 2000 | 2 | 1 | 未定 |
| 製品B | 2500 | 1 | 2 | 未定 |
| 製品C | 6000 | 4 | 3 | 未定 |
ただし原材料は100kgしかなく、生産時間は50hしかありません。どの商品を生産すべきでしょうか?あるいは複数の商品を生産するという道筋はあるのでしょうか?
この場合、利益を最大化するための製品A、B、Cの最適な生産量を求めるために、ソルバーを使用します。ソルバーは複数の変数(ここでは製品A、B、Cの生産量)を同時に調整し、一方で複数の制約(原材料の必要量、生産時間)を満たす最適な解を見つけることが可能です。このような問題は、ゴールシークだけでは解くことができません。
具体的には、次のようにします:
利益を計算するためのセルを作成します。それぞれの製品の利益は「生産量」×「単位あたりの利益」なので、それらをすべて加えたものが全体の利益になります。この計算を行うセル(例えば、セルB6)に以下のような計算式を設定します。ただし計算をする前にそれぞれの「生産量」欄へ「1」などの適当な値いを入れておくとわかりやすいでしょう。
利益:=B2*E2 + B3*E3 + B4*E4
またここでは原材料の利用可能量と生産時間が限られているとします。この計算を行うセル(例えば、セルB7とB8)に以下のような計算式を設定します。
原材料合計:=C2*E2 + C3*E3 + C4*E4 生産時間合計:=+D2*E2 + D3*E3 + D4*E4
それぞれの生産量を1と仮定していときはB6:B8に以下のように表示されます。
| 利益 | 100 |
|---|---|
| 原材料合計 | 7.5 |
| 生産時間合計 | 6 |
ソルバーを起動し、「目的セルの設定」には全体の利益を計算するセル(B6)を、「目標値」は「最大値」を選択します。
「変数セルの変更」には製品A、B、Cの生産量を表すセル(E2:E4)を選択します。
制約条件を設定します。例えば、原材料の利用可能量が100kg、生産時間が50時間であるとすると、それぞれの製品について、「生産量」×「単位あたりの原材料の必要量」が100kg以下、また「生産量」×「単位あたりの生産時間」が50時間以下でなければなりません。そのため、以下のような制約条件を設定します:
B7<=100 B8<=50
そして、ソルバーを実行します。ソルバーは制約条件を満たしつつ、全体の利益を最大化する製品A、B、Cの最適な生産量を計算します。この条件では製品Aに注力するのがよいとの計算結果がでます(製品Aが50個、他は0個)。
以上の設定と手順で、製品の最適な生産量を決定することが可能です。なお、実際の問題では、利用可能な原材料の量や生産時間などの制約条件は具体的な数値で与えられるはずです。また、製品の生産量は通常、0以上の整数値をとると考えられるので、その点も制約条件として設定することが考えられます。

コメント